Flipped Classes Part 4: How to Flip a Lesson

-

 In part 1 of this series, we talked about what a flipped class is. In part 2 I gave you a list of things you should consider when planning your flip. In part 3 we talked about getting student buy-in. Now, it's finally time to see it in action. How do I actually turn my lecture notes into a flipped lesson?

Here are a few general considerations to get you started before we jump into the example:

  1. Work from concrete to abstract. Give students very concrete examples and exercises to work with in the pre-class. That will put them in a strong position to move to a more abstract understanding when you meet together as a class.
  2. Students can read definitions and formulas. They may not yet understand the concepts totally, but they certainly are capable of writing them down without you putting them on the board. This is an excellent task for the pre-class activities.
  3. Avoid "tricky" problems in the pre-class activities. While students are not expected to fully absorb the topics before class, they should be able to build a little bit of confidence.  Try to make the problems very straightforward. You can tackle the tricky or complicated versions in class.
  4. The pre-class is a great place to review or connect to past topics. Much of what we do in our classes either builds on past topics or at least has some connection to them. Often, we don't have enough time to review in class or make those connections explicit. However, students can get a lot of value from reviewing it in the pre-class.
  5. Give students a place to ask questions before class. I picked this one up from Dr. Michael Weingart at Rutgers. Not only does this set the expectation that students do not understand everything before coming to class, but it also provides us as instructors a great way to start the class meetings. What a valuable learning opportunity for everyone!
Alright, let's get into the example. I'm going to use my lesson on systems of linear equations in two variables from my College Algebra class to show you how I would turn lecture notes into a flipped lesson. In the fall, despite how much I value and enjoy flipped classes, I ended up mostly just traditionally lecturing by the end of the semester. This year, however, I did manage to keep up my commitment to active learning all semester long. So, both versions that you'll see are from the exact same class, taught in back-to-back semesters, both during the pandemic. They are both lessons that I actually implemented with students, and I would still say that neither is perfect, yet. I definitely already have some things I want to change about my flipped design, but I'll say some more about that at the end.

The Lecture Notes

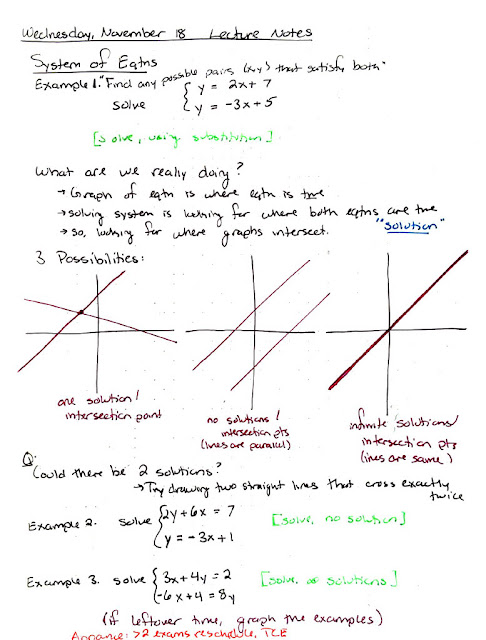
Without further ado, here are my lecture notes on systems of equations from last fall:

Let me say a few things about these notes before I explain how I completely changed them. First, notice that I began by focusing on just how to solve the problem when everything works. Namely, when there is a single solution. I do still like this being emphasized first. In lots of topics, we often like to give the most general description possible and then all of our examples are some versions of that. However, I'm pretty sure our brains don't like that when we're first learning. Let's start by understanding an algorithm or idea in the nice case. Once you understand that, it is much easier to understand the exceptional, extreme, or broken cases and understand why those cases need special attention.

Next, I want to point out how I really wanted students to understand why there are only three cases, in terms of the graph. This is very important to me, and I just didn't have time to say much about it when I had to fit that and three examples into a 50-minute lecture. I thought about this a lot when I designed my flip, so you'll see that I ended up really emphasizing it.

One thing I don't like about the way I planned this is the way that the term "solution" gets buried. The general action of what I expect them to do when I say "Solve the following system" does, I think, get through, but I want students to understand more than just the process that a certain phrase indicates.

You might even notice my note at the end about graphing the last two examples if there is time. There wasn't time.

The Flip

Let me lay out a few of my goals and decisions when designing this flip.

First, one of my big goals throughout the semester this spring was for students to understand the connection between a formula or equation and its graph. It has become more and more clear to me that when students enter College Algebra, graphs and formulas are just two totally separate topics in their minds. Not only does this deprive them of an excellent tool for making connections and the opportunity to understand the concepts in multiple ways, but it actually explicitly hinders them from understanding some of the topics in the course. Since they had seen this throughout the semester, I made this a big focus of the pre-class work and the warm-up activity I started class with.

Second, I wanted to emphasize the idea of what a solution is much more than I did before. Partly this is because understanding definitions is just part of learning the material. But more than that, it really helps students remember and understand how to solve the problems. For example, if students really fundamentally understand what a "solution" to an equation or a system of equations is, then the last step of plugging in to find the other variable is just logical: the thing I'm looking for is an ordered pair but I only have one number so far. I need to do something to find the other number. On the other hand, if students are relying entirely on remembering the algorithm, that just becomes another step they have to not forget.

Third, I wanted to keep my emphasis on understanding the "nice" case first before tackling the exceptional cases. I may have taken this too far because I barely had time to say anything about those exceptional cases. I'll say more about that later.

Pre-Class

I have been using the OneNote Class Notebook for my pre-class notes. I load the notes into each student's notebook so they can write/draw all over them while working through them. They usually follow the same pattern: I introduce an idea or definition, then give them either a written or video example, then give them a problem to try with the solution written further down. For this case, I had two iterations of this sequence. First, reviewing what a solution to an equation is:


Second, discussing what a solution to a system of equations is:


At the end of the notes, I have a form where they can submit questions before class that I go over at the start of class. I did not get any questions for these notes, though I think some of that is just the usual end-of-semester fatigue. I haven't been getting any questions at all from these forms for a few weeks.

After working through the notes, I have students complete a quiz on Canvas, which I built using the New Quizzes tool. They have unlimited attempts and only the highest score is kept. With the new quizzes tool, I can require a wait time in between attempts, which encourages students to look back through their notes before trying it again. Of course, for that to work, all of the problems are computer-graded. Here were the questions I asked for this assignment:


In-Class

Since I've been teaching simultaneously online and in person, I spent a lot of time looking for a tool for active learning that would work for both. I landed on Desmos activities, and ended up totally loving them, even for a more traditional semester. I'll write a longer post on that later.

The general format for the class meetings is always the same: students open up the Desmos for the day where they start with a brief check-in ("How are you feeling today?") and then work on some warm-up problems that are either review from the pre-class, review from a previous class, build on the pre-class, or some combination of all of those. I often build those warm-up problems myself, and students have reported really appreciating when they include some self-checking so that they have a good sense of their own understanding before jumping into the new material for the day. 

For this particular topic, I was delighted to find that there are a few excellent activities on linear systems already published on the Desmos website that fit my desired organization of the material. So, their warm-up slides were all just directly from an activity on understanding what solutions to linear systems are both graphically and algebraically. The algebraic part was a review of what they did in the pre-class and then the graphic part built on that. 

After going over the warm-up, I showed them an example of solving a system of linear equations using substitution. The few students who were in the classroom with me indicated that they followed what I was saying and why that process made sense. If you are curious, here is the actual notes I wrote during class, displayed on the doc cam:


I then sent them back to the Desmos to work on the other half of the activity for today, also pulled from an excellent activity already published by Desmos. We spent most of the rest of class on this, and I was generally impressed with the work students were submitting.

I did stop them a few minutes early to give a quick discussion about what can go wrong (i.e. when there are infinitely many solutions or when there is no solution). We didn't do any examples of that, but here are the notes that I wrote on the doc cam:


While I don't yet think I'm satisfied with this setup, because I didn't have much time to discuss the weird cases, I really like what the students were able to accomplish in this lesson. Their homework on the material is due tonight, and I have office hours this afternoon, so I suppose time will tell!

Reflections

Remember how I said I really wanted students this semester to understand the connection between a graph and an equation? Well, some of the answers in the warm-up activity really have me deeply impressed at their progress on that goal. One of the slides asked students "What does it mean for a point to be a solution to a linear equation? For example, if I say, '(2,5) is a solution to the equation y=2x+3,' how could you check my claim?" Here are a few of the responses I got:

  • You plug the point into the equation and if it solves equally, then the point is a solution. 
  • Plug in 2 where x is and 5 where y is. if they do not equal it is not a solution. 
  • type it into desmos and check, or plug in 2 for x and see if the solution is 5
  • No that is not correct because when you plug it in you get 5=7.
  • not equal you can replace 2 with 1

Wow. Just wow. I spent a lot of time telling them how impressed I was before we moved on from the warm-up. 

We also talked about one of the other slides in the warm-up, which showed students a graph of two lines that are not parallel but do not intersect within the window shown. It asked students if the system has a solution. The results were mixed, and the explanations students gave really showed their thinking, like this one from a student that said no: "on this view of the graph you aren't able to see any intersecting points which means there is no solution for the system of equations, but it could intersect each other at a different view." This lead to a great discussion on the difference between asking whether a solution exists or asking if we can identify it/see it. 

All of this within the first 15 minutes of class. Starting to see the real, concrete opportunities of a flipped class?

Now, one of the things I was a bit disappointed about with this plan is that we didn't get much time to talk about the exceptional cases, and absolutely no time to practice word problems. I do think that compromising the practice on the core stuff would not be worth what they could get out of practice on the weirder parts. If they understand what solutions are and how to find them when things work out nicely, then they have a better foundation to understand the less nice parts. But if I could just somehow find more time, that would be great.

Maybe next semester I'll move some more of the beginning of class stuff to the pre-class. In this lesson, my pre-class really just focused on understanding what a solution is algebraically, but I could easily add the graphic perspective there as well. I could maybe even introduce the technique of solving using substitution in the pre-class. There are lots of great videos out there that would be just as good as my live example during class.  Though this would greatly increase the workload of the pre-class work, so I would have to back off the homework. Remember how workload is a really important consideration when flipping? I think I've now officially said that in every part of this series...


Well, that's it. That's all four parts. I'm sure I'll do an update this fall because I already have lots of ideas to change things. But I hope this gives you what you need to get started. What classes are you going to flip?

Comments

Post a Comment

Popular posts from this blog

Flipped Classes Part 2: 5 Things to Consider When Flipping your Class

-
So, in part 1 of this series,  I introduced how I define a flipped class. Along the way, I mentioned a few things that need further details. As promised, here they are! So, without further ado, here are 5 things you need to consider when flipping your class. 1. Student Time I made this first because it's so incredibly important but also the easiest one to forget. Despite all of the benefits of a flipped class, we don't get to ask for more time from students. So, if you are going to require students to do something before class, that absolutely has to be offset by how much is required of them after class. Some of the time they would normally spend on their homework is offset by the fact that they have already gotten some practice during class, but this is a pretty small amount. Generally, the rule of thumb is that for every credit hour the course is, you can require 3 hours per week of student time for the median student. In fact, for lots of universities, this is written as p...
Read more

Flipped Classes Part 3: Do's and Don'ts of Getting Student Buy-In

-
 The first time I heard about the idea of flipped classes, I thought they were incredibly stupid. "But then they're not teaching you!" I said. Obviously, my perspective on this has changed. I now often reflect on why I started out with that perception, and I can almost surely point it to how it was described to me. At the time, I was an undergraduate student working in the on-campus tutoring center. The department was piloting a flipped version of one of the courses for which we get many students in the tutoring center. One of the students who was in this class was in the center one night asking for help. She described the course as the students having to teach themselves from the videos and then they just do homework during class. Looking back, I doubt this was actually the instructor's plan nor was it probably the way it was explained to students. However, this was how that particular student understood it and explained it to me. I tell you this story to illustrate ...
Read more

My Teaching Philosophy

-
 As I begin this blogging adventure, I thought it would make sense to start by outlining my teaching philosophy. There are four basic parts to the "why" of how I teach, outlined below. You must do mathematics to learn mathematics. Seems obvious, right? Yet, our default way of teaching mathematics is to talk mathematics at students, or lecture. Don't get me wrong, I've fallen into this trap. By virtue of being the teacher, we know what we are talking about, so talking about it is the easiest way to present content. However, it is also probably the most inefficient way to teach, for teaching cannot happen if learning does not happen. Lecturing is an instructor-focused activity. Learning, however, is an internal process. Students need to be working their own brains in order to learn, not passively listening to someone else. In my classrooms, I put student thinking and exploration as the focus of class time. That is not to say that I don't ever lecture. In fact, I...
Read more